Bar "Jus de fruit pour avoir la pression osmotique"
Méthode : Racines d'une équation : code Python
Nous allons chercher à résoudre 1 équation à 1 inconnu avec Python à l'aide de la fonction fsolve de la librairie Scipy.
Pour illustrer ce type de calcul, nous allons chercher pour quelle concentration la pression osmotique du jus de fruit atteint la valeur de 33 bars.
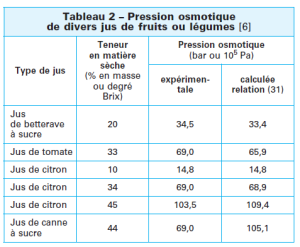
Nous avons la relation suivante pour la pression osmotique du jus de fruit : \(Π(πππ)=\frac{133.75π}{100−π}\) avec c concentration en % massique (selon la relation empirique de Thijssen présentée sur les Techniques de l'Ingénieur J2789 p10 voir figure ci-contre)
Il s'agit donc de résoudre l'équation suivante : \(\frac{133.75π}{100−π}−33=0\)
Ceci peut se faire en 6 lignes sous Python en introduisant la fonction PI pour laquelle il faut trouver la racine .
from scipy.optimize import fsolve
def PI(c):
PIc=(133.75*c/(100.-c))
return PIc-33
c=fsolve(PI,1)
print ('La concentration massique est de :',c[0], '% massique')
Cette pression osmotique et cette concentration de 19,8 % correspondent à du jus de betterave à sucre.
Il peut être intéressant de faire passer la valeur à obtenir en argument de la fonction afin de pouvoir utiliser la fonction pour faire des calculs de concentration pour différentes valeurs de pression osmotique (c'est ce que nous ferons dans l'étude de la concentration de polarisation). Le code modifié est utilisé ici pour calculer la concentration correspondant à une pression osmotique de 66 bars.
PI_cible=66.
def PI(c, PI_cible):
PIc=(133.75*c/(100.-c))
return PIc-PI_cible
c=fsolve(PI,1, args=PI_cible)
print ('La concentration massique est de :',c[0], '% massique')
Cela correspond à 33,04 % massique c'est à dire du jus de tomate !